finding probability without replacement

reph Maret 08, 2022 finding , probability , without Comment

For a I used the equation nCk Pk Q n-k and got P X0 036 P X1 048 P X2 016. Method 2 Without replacement.

Probability Without Replacement Video Lessons Examples And Solutions

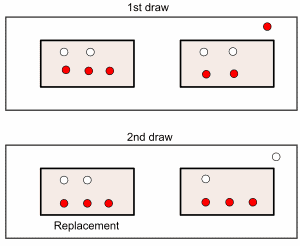
A marble is drawn from the bag replaced and another marble is drawn.

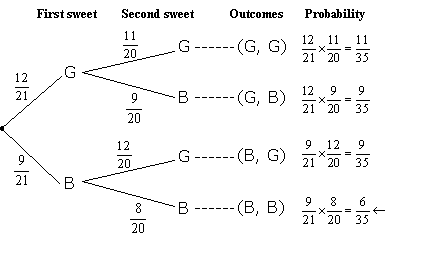
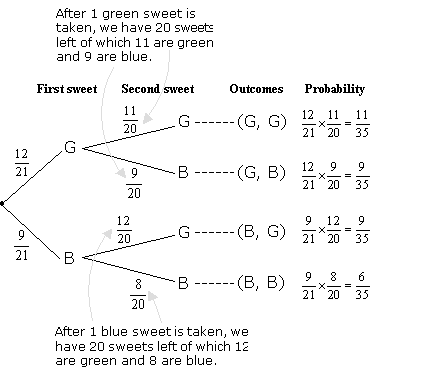
. All the branches are multiplied by adding them vertically to find the final probability of the result. So the probability is. All the branches of a specific outcome are looked for.

From the above example we note that probability with replacement. P AB P A P BA Note that P BA is the conditional probability of event B occurring given event A occurs. Displaying top 8 worksheets found for probability with and without replacement.

One example uses With Replacement and one example uses Without Replacementmathematics probability. Draw the Probability Tree Diagram and write the probability of each branch. P 4 false positives 5 98 4 97 3 96 2 95 0000001384.

School Picking Without Replacement When picking n items out of N total items where m of them are distinct the odds of picking exactly k distinct items is defined as. For example if A 1 2 3 and k 2 there are 6 different possibilities. Look for all the available paths or branches of a particular outcome.

Iii at least two green balls are drawn given that at least one of each colour is drawn. Using this rule all of these events would be considered unusual. What is the probability of finding the two defectives in exactly three attempts.

Calculate the probability of drawing a black marble if a blue marble has been withdrawn without replacement the blue marble is removed from the bag reducing the total number of marbles in the bag. For example the probability of choosing the name Tyler is 15 on the first draw and the probability of choosing the name Ando is 14 on the second draw. P AB P A P B If A and B are dependent then the formula we use to calculate P AB is.

The tree diagram of probability is drawn and the probability related to each branch is noted down. Today were going to learn how to find probability from a frequency table for selections with and without replacement. In general we can argue that there are k positions in the chosen list.

5 good and 2 defective bulbs are mixed. Finding the percentile of a normally distributed variable. But the solution key tells me that P X0 03 P X1 06 P X2 01.

The probability of drawing two aces without replacement is 452 x 351 1221 or about 0425. Draw a ball and it could be red or white. For example if we draw a candy from a box of 9 candies and then we draw a second candy without replacing the first candy.

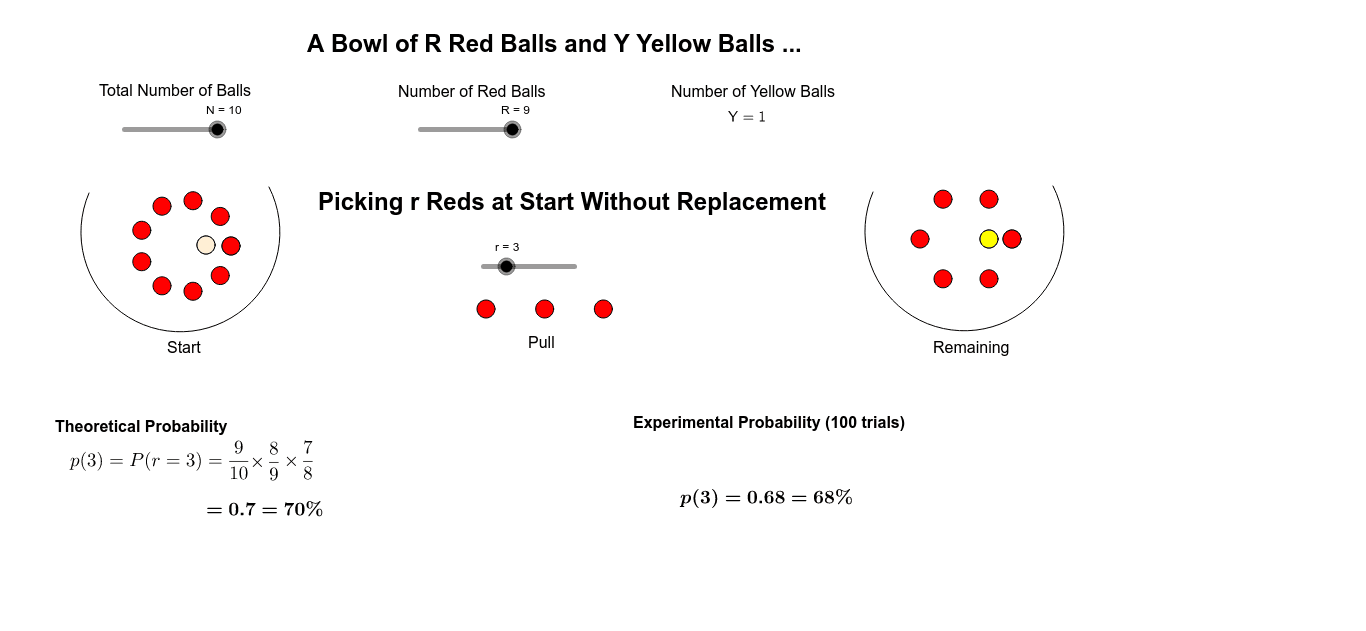
210 x 39 690 or 115 67 Compare that with replacement of 6100 or 6 House of cards activity using probability without replacement. When we sample without replacement the items in the sample are dependent because the outcome of one random draw is affected by the previous draw. Consider the same setting as above but now repetition is not allowed.

Without replacement dependent events Ptwo reds 36⅖⅕. As a good rule of thumb if something occurs less than 5 of the time ie probability 005 we often call it unusual. We see directly from the problem above that what we choose to do with replacement has bearing on the values of probabilities.

P 3 false positives 5 98 4 97 3 96 000006575. Find the probability that. I all the balls are green.

Finding probability without replacement for choosing light bulbs. In other words an item cannot be drawn more than once. And best of all they all well most come with answers.

This video goes through 2 examples of Probability. Probability without replacement means once we draw an item then we do not replace it back to the sample space before drawing a second item. Ii at least one ball of each colour is drawn.

Let n 2 number of trials P 25 probability of success Q 35 probability of failure k number of success. A Bag contains 4 red balls and 6 green balls. 4 balls are drawn at random from the bag without replacement.

212 Ordered Sampling without Replacement. Probability of drawing a blue marble. Take the example of a bag of 10 marbles 7 of which are black and 3 of which are blue.

The probability of choosing the blue ball is 210 and the probability of choosing the green ball is 39 because after the first ball is taken out there are 9 balls remaining. A Calculate the probability that. Assume that orders are randomly selected from those included in the table.

Two letters are chosen without replacement at random from the english alphabet. B Are the events at least two green balls are drawn and at least one ball of each. Do not replace the ball from the first draw and draw another ball that could again be either red or white.

Multiply along the branches and add. Use the data in the following table which lists drive through order accuracy at popular fast food chains. Position 1 Position 2 Position k.

Remember that the objects are not. Heres our problem statement.

Probability Without Replacement Youtube